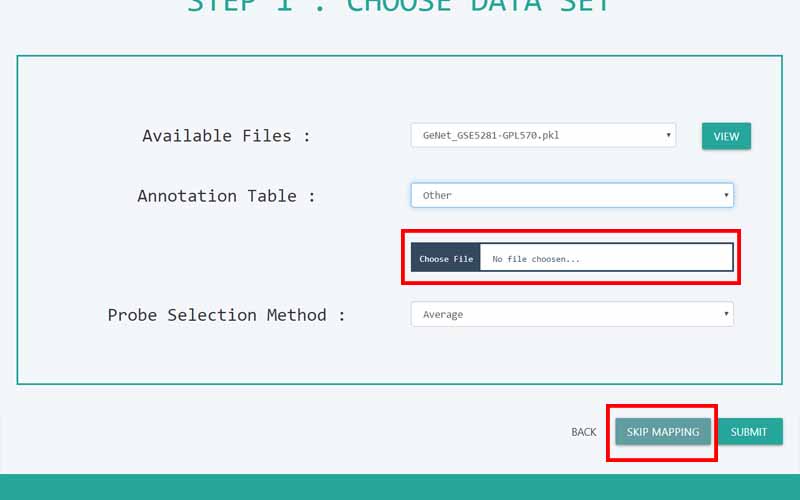
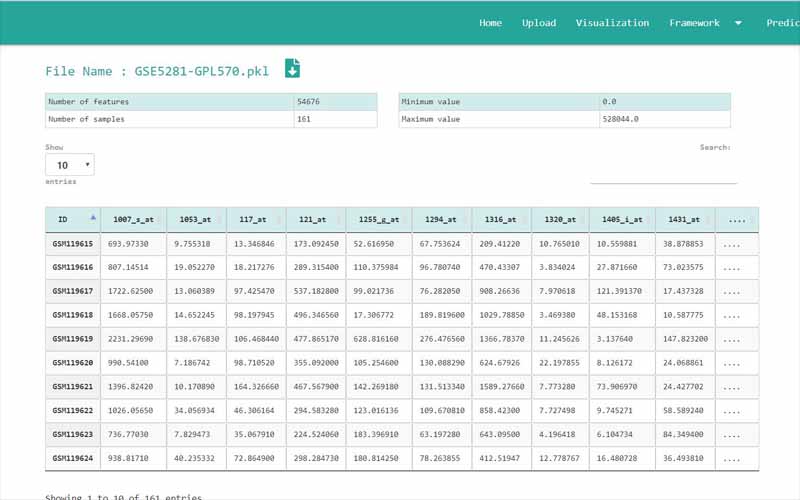
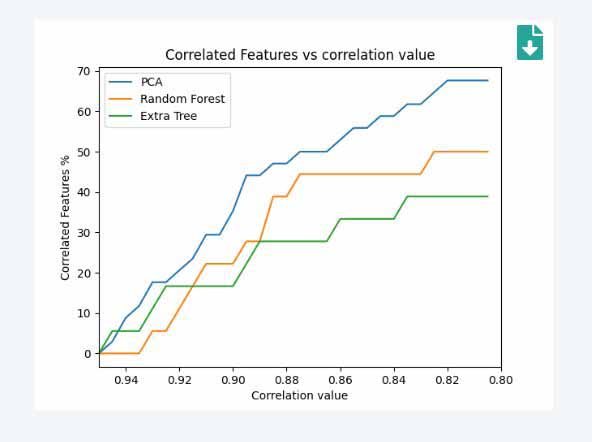
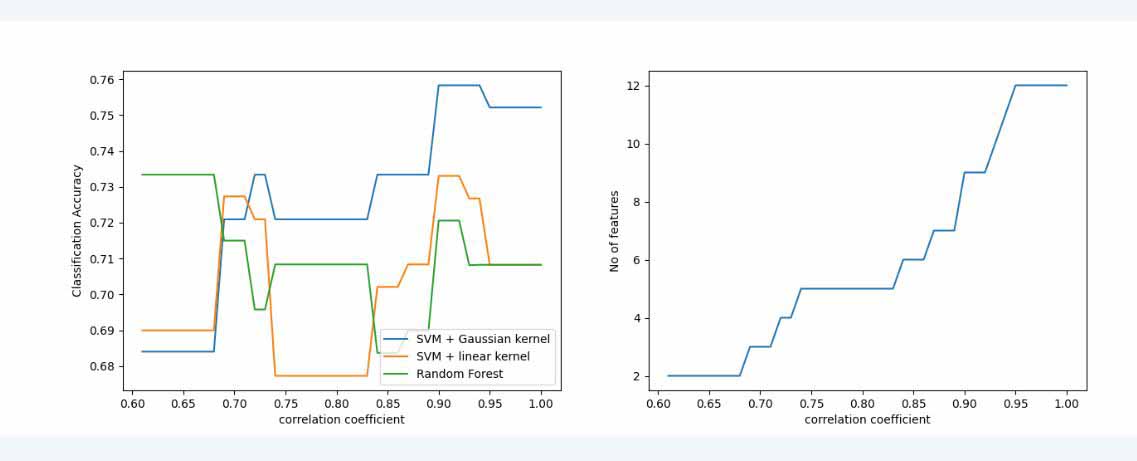
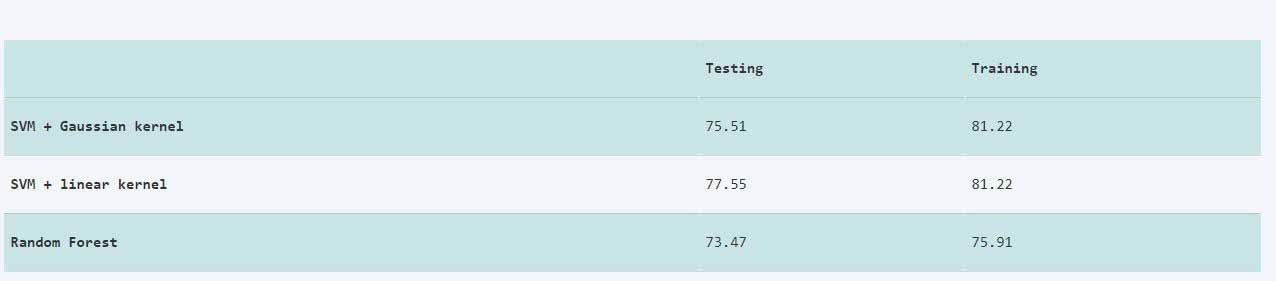
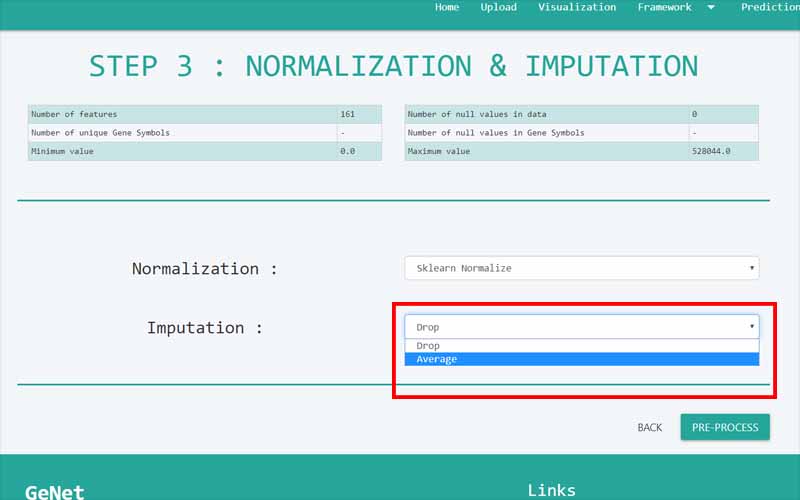
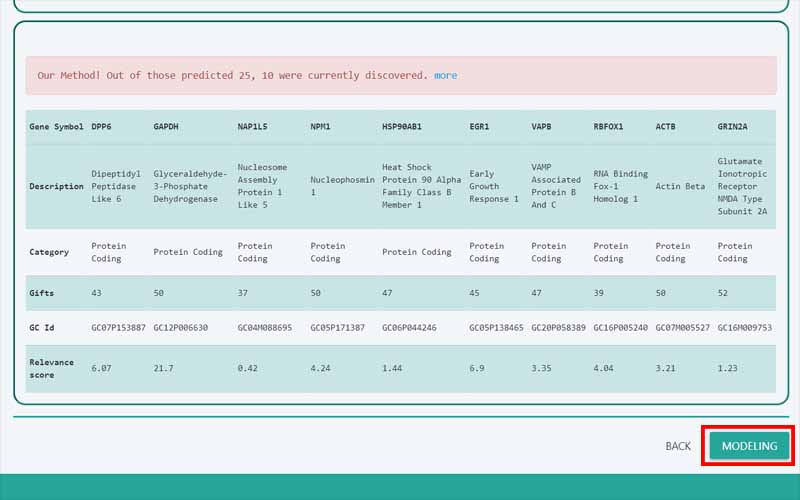
Upload Files

You can only upload files in comma-separated value (.csv) files. The files you upload should be in the following format. We have provided you with a sample file obtained from the NCBI GEO database. It is a dataset containing information about 161 samples with 87 Alzheimer disease patients and 74 normal samples.
01. The first column of the file refers to the unique ID of the samples (In here the number of samples is 161). For example, here the IDs are GSM119615, GSM119616, GSM119617, GSM119618, etc. Note that the sample IDs are used only for naming purposes. Therefore, the sample IDs can be any unique name.
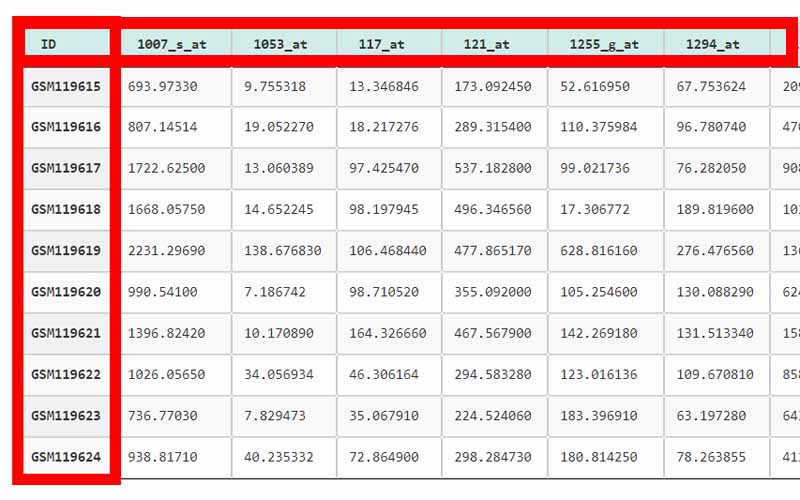
02. The column headers(except the first column) contains the Probe IDs. A probe ID is a unique ID given for a probe/spot in
. For example, here the probe IDs are 1007_s_at, 1053_at, 117_at, etc.03. A row represents the gene expression data values of all the probe IDs with respect to a given sample. This highlighted row represents the gene expression data values for every probe ID in the sample GSM119618.
04. The cells in the highlighted area can only contain numerical values. They contain gene expression values of the samples tested upon different probe_IDs.

05. Important: There are two types of data sets that can be used in GeNet. Apart from the data sets that have to be used in the “Prediction” step, all the other data sets should include their last column named “class”. GeNet supports only binary status for the class label. That is, the samples should either be disease positive or disease negative. The negatives should be represented by 0 while the positive values should be represented by 1. For example, in the given Alzheimer disease-related data set, 1 corresponds to the samples of patients having the disease. 0 corresponds to the control samples. Note that this column should be named as ‘class’ all in simple letters.
For the data sets that can be used in the “Prediction” step, the column containing the “class” label is not necessary. For every other step in GeNet, the data set should include its last column with the binary status.